Prof. Dr. Balázs Kovács

Numerics of partial differential equations

Phone:
+49 5251 60-1839
ORCID:
0000-0001-9872-3474
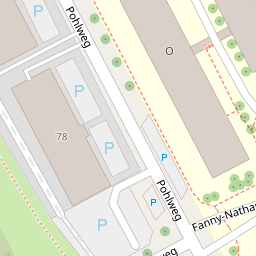
Office Address:
Warburger Str. 100
33098 Paderborn
Room:
J2.241

About Balázs Kovács

Curriculum Vitae

Since 01.07.2023: Professor (W3) for Mathematics and its applications

Paderborn University

2023-2026 Heisenberg-Professor

01.10.2020 - 30.06.2023: DFG Heisenberg Position holder

University of Regensburg, Germany
German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) Project-ID 446431602

01.04.2022 - 30.09.2022: Substitute Professor (W2)

Technical University of Munich
substituting Prof. Caroline Lasser

01.07.2015 - 30.09.2020: PostDoc

University of Tübingen

Mentor: Prof. Christian Lubich

18.12.2018: Habilitation

University of Tübingen

03.03.2016: PhD degree

01.10.2014 - 30.06.2015: DAAD Scholarship

University of Tübingen

01.04.2014 - 30.09.2014: ERASMUS Stipendium

University of Tübingen

01.09.2011 - 31.07.2014: PhD candidate

ELTE Eötvös Loránd University, Budapest, Hungary.

Supervisor: Prof. János Karátson
Dissertation: Effcient numerical methods for elliptic and parabolic partial differential equations

01.09.2009 - 15.07.2011: Applied Mathematics MSc

ELTE Eötvös Loránd University, Budapest, Hungary.

01.09.2006 - 15.07.2009: Mathematics BSc

ELTE Eötvös Loránd University, Budapest, Hungary.

Research

Research Interests

My research focuses on the numerical analysis of algorithms for geometric surface flows and for evolving surface partial differential equations, e.g. mean curvature flow, Willmore flow, inverse mean curvature flow, and geometric flows coupled to surface processes.

I am interested in time discretisation methods, numerical methods for parabolic and wave-type problems with dynamic boundary conditions, numerical analysis for Maxwell's equations with various boundary conditions.

○ My research project on geometric surface flows is funded by the Heisenberg Programme of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – titled Numerical analysis of geometric flows and evolving surface partial differential equations (2020–2026, Project ID: 446431602).

○ For the second funding period (2022–2023) I was a principal investigator within the DFG Research Training Group 2339 – Interfaces, Complex Structures, and Singular Limits (Project ID: 321821685).

○ For the second funding period (2023–2025) Sören Bartels and I will have a joint project in the DFG Research Group 3013 Vector- and Tensor-Valued Surface PDEs (Project ID: 417223351).

Publications

Latest Publications

Numerical analysis of an evolving bulk--surface model of tumour growth
D. Edelmann, B. Kovács, C. Lubich, ArXiv (2024).
DOI
Numerical surgery for mean curvature flow of surfaces
B. Kovács, SIAM Journal on Scientific Computing 46 (2024).
DOI
Error analysis for the numerical approximation of the harmonic map heat flow with nodal constraints
S. Bartels, B. Kovács, Z. Wang, IMA Journal of Numerical Analysis (2023).
DOI
Error analysis of BDF 1-6 time-stepping methods for the transient Stokes problem: velocity and pressure estimates
A. Contri, B. Kovács, A. Massing, ArXiv (2023).
DOI
Viscoelastic Cahn–Hilliard models for tumor growth
H. Garcke, B. Kovács, D. Trautwein, Mathematical Models and Methods in Applied Sciences 32 (2022) 2673–2758.
DOI
Show all publications

Teaching


Current Courses

  • Vorlesung Numerik
  • Seminar "Algorithmen aus dem Buch"
  • Oberseminar

Scientific Engagement

01.10.2021 - 30.06.2023  |  Member of the Faculty Board at the University of Regensburg

representing academic staff